MergeSort

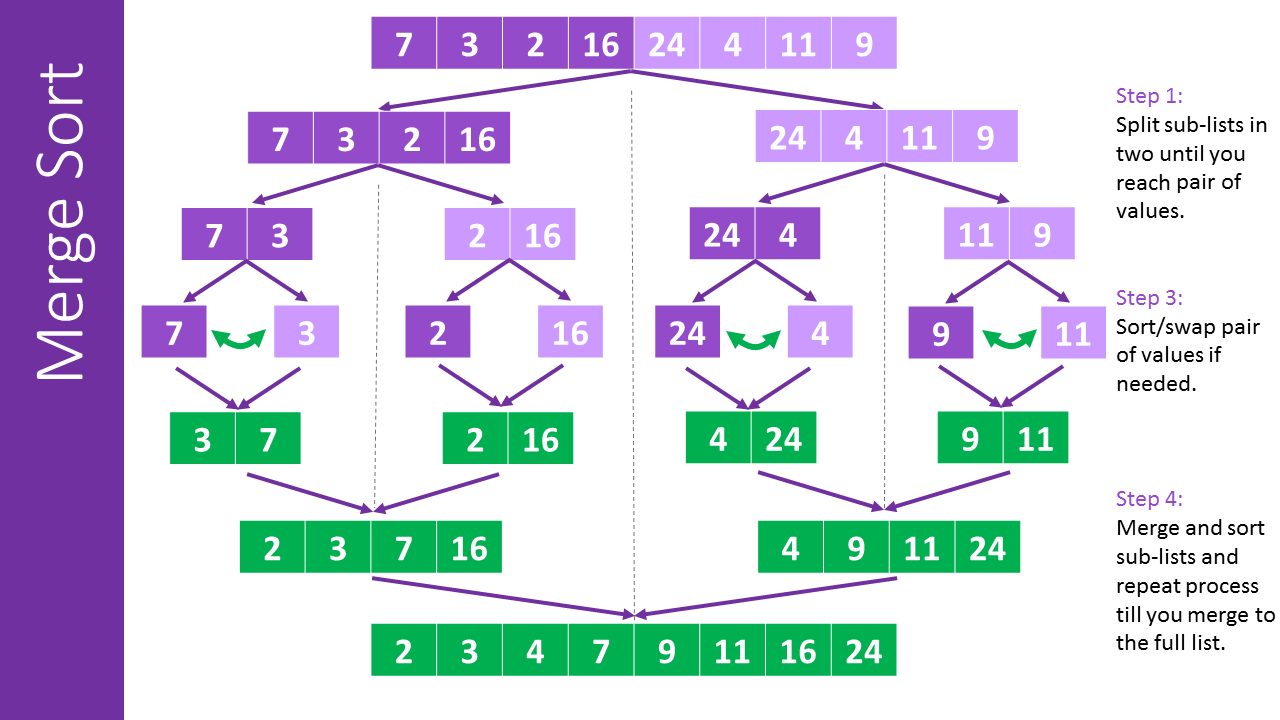
This algorithm is a combination of two things - merging and sorting. It exploits the fact that arrays of 0 or 1 element are always sorted,
and works by decomposing an array into smaller arrays of 0 or 1 elements, then building up a newly sorted array.

MergeSort Pseudocode

1. Break up the array into halves until you have arrays that are empty or have one element.
2. Once you have smaller sorted arrays, merge those arrays with other sorted arrays until you are back at the full length of the array.
3. Once the array has been merged back together, return the merged (and sorted!) array.

MergeSort Implementation

JavaScript

function Merge(arr1, arr2){
    let n = arr1.length;
    let m = arr2.length;
    let i = 0;
    let j = 0;
    let arr = [];
    while( (i < n) && (j < m)){
        if(arr1[i] < arr2[j]){
            arr.push(arr1[i]);
            i++;
        } else{
            arr.push(arr2[j]);
            j++;
        }
    while(i < n){
        arr.push(arr1[i]);
            i++;
    }
    while(j < m){
        arr.push(arr2[j]);
            j++;
    }
    return arr;
}
function mergeSort(arr){
    if(arr.length === 1) return arr;
    let mid = Math.floor(arr.length / 2);
    let left = mergeSort(arr.slice(0, mid));
    let right = mergeSort(arr.slice(mid));
    return merge(left, right);
}

Python

import math
def merge(arr1, arr2):
    n = len(arr1)
    m = len(arr2)
    arr = []
    i = 0
    j = 0
    while (i < n) and (j < m):
        if arr1[i] < arr2[j]:
            arr.append(arr1[i])
            i += 1
        else:
            arr.append(arr2[j])
            j += 1
    while i < n:
        arr.append(arr1[i])
        i += 1
    while j < m:
        arr.append(arr2[j])
        j += 1
    return arr
def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = math.floor(len(arr)/2)
    left_arr = merge_sort(arr[:mid])
    right_arr = merge_sort(arr[mid:])
    return merge(left_arr, right_arr)

Time Complexity: Big(O)

Worst case: O(N log(N))